Optimizers

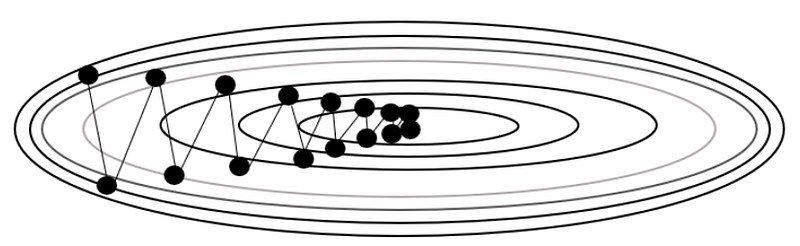
Optimizers are algorithms or methods used to minimize an error function(loss function)or to maximize the efficiency of production. The purpose of neural network learning is to find the parameters that make the value of loss function as small as possible. This is the problem of finding the optimal parameters. The process of solving this problem is called optimization.

The four optimizers the post mainly deals with are as follows:

• Stochastic Gradient Descent (SGD)
• Momentum
• AdaGrad
• Adam

This post will discuss and compare these optimizers. the book Deep Learning From Scratch, published by O’Reilly in September 2019.

Stochastic Gradient Descent (SGD)

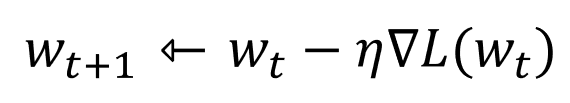
Stochastic gradient descent(SGD) is an iterative method for optimizing an objective function with suitable smoothness properties . SGD performs a parameter update for each training example x and label y.

class SGD:

def __init__(self, lr=0.01): 
        self.lr = lr 
         
    def update(self, params, grads): 
        for key in params.keys(): 
            params[key] -= self.lr * grads[key]

Momentum

Momentum is a method that helps accelerate SGD in the relevant direction and dampens oscillations.

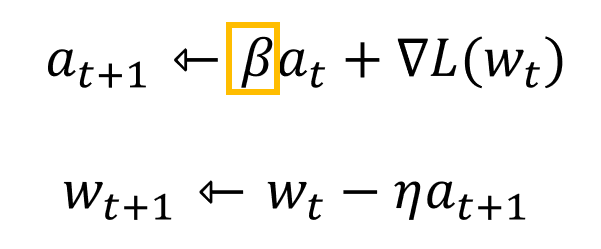
class Momentum:

def __init__(self, lr=0.01, momentum=0.9): 
        self.lr = lr 
        self.momentum = momentum 
        self.v = None 
         
    def update(self, params, grads): 
        if self.v is None: 
            self.v = {} 
            for key, val in params.items():                                 
                self.v[key] = np.zeros_like(val) 
                 
        for key in params.keys(): 
            self.v[key] = self.momentum*self.v[key] - self.lr*grads[key]  
            params[key] += self.v[key]

AdaGrad

Adagrad is an algorithm for gradient-based optimization. It adapts the learning rate to the parameters, performing smaller updates for parameters associated with frequently occurring features, and larger updates for parameters associated with infrequent features.

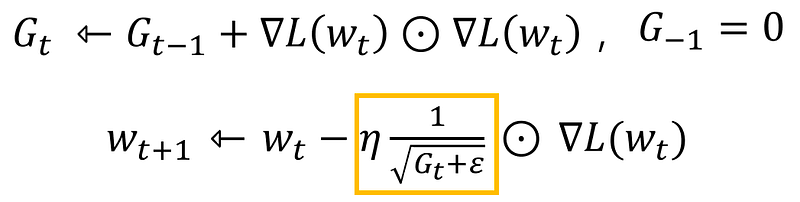
class AdaGrad:

def __init__(self, lr=0.01): 
        self.lr = lr 
        self.h = None 
         
    def update(self, params, grads): 
        if self.h is None: 
            self.h = {} 
            for key, val in params.items(): 
                self.h[key] = np.zeros_like(val) 
             
        for key in params.keys(): 
            self.h[key] += grads[key] * grads[key] 
            params[key] -= self.lr * grads[key] / (np.sqrt(self.h[key]) + 1e-7)

Adam

Adaptive Moment Estimation (Adam)is a method that computes adaptive learning rates for each parameter. In addition to storing an exponentially decaying average of past squared gradients vt like Adadelta and RMSprop, Adam also keeps an exponentially decaying average of past gradients, similar to momentum.

class Adam:

"""Adam (<http://arxiv.org/abs/1412.6980v8>)"""

def __init__(self, lr=0.001, beta1=0.9, beta2=0.999): 
        self.lr = lr 
        self.beta1 = beta1 
        self.beta2 = beta2 
        self.iter = 0 
        self.m = None 
        self.v = None 
         
    def update(self, params, grads): 
        if self.m is None: 
            self.m, self.v = {}, {} 
            for key, val in params.items(): 
                self.m[key] = np.zeros_like(val) 
                self.v[key] = np.zeros_like(val) 
         
        self.iter += 1 
        lr_t  = self.lr * np.sqrt(1.0 - self.beta2**self.iter) / (1.0 - self.beta1**self.iter)          
         
        for key in params.keys(): 
            #self.m[key] = self.beta1*self.m[key] + (1-self.beta1)*grads[key] 
            #self.v[key] = self.beta2*self.v[key] + (1-self.beta2)*(grads[key]**2) 
            self.m[key] += (1 - self.beta1) * (grads[key] - self.m[key]) 
            self.v[key] += (1 - self.beta2) * (grads[key]**2 - self.v[key]) 
             
            params[key] -= lr_t * self.m[key] / (np.sqrt(self.v[key]) + 1e-7) 
             
            #unbias_m += (1 - self.beta1) * (grads[key] - self.m[key]) # correct bias 
            #unbisa_b += (1 - self.beta2) * (grads[key]*grads[key] - self.v[key]) # correct bias 
            #params[key] += self.lr * unbias_m / (np.sqrt(unbisa_b) + 1e-7)

Comparison of Optimizers

Let’s compare the 4 types of optimizers.

def f(x, y): 
    return x**2 / 20.0 + y**2

def df(x, y): 
    return  x / 10.0, 2.0*y

init_pos = (-7.0, 2.0) 
params = {} 
params['x'], params['y'] = init_pos[0], init_pos[1] 
grads = {} 
grads['x'], grads['y'] = 0, 0

optimizers = OrderedDict() 
optimizers["SGD"] = SGD(lr=0.95) 
optimizers["Momentum"] = Momentum(lr=0.1) 
optimizers["AdaGrad"] = AdaGrad(lr=1.5) 
optimizers["Adam"] = Adam(lr=0.3)

idx = 1

# Figure Size 
fig, ax = plt.subplots() 
fig.set_size_inches(10, 10)

for key in optimizers: 
    optimizer = optimizers[key] 
		x_history = []  
    y_history = []  
    params['x'], params['y'] = init_pos[0], init_pos[1]

for i in range(30): #30 steps 
        x_history.append(params['x']) # -7.0 
        y_history.append(params['y']) # 2.0

# Set the initial position each iteration  
        grads['x'], grads['y'] = df(params['x'], params['y']) # -7.0, 2.0 
        # df is gradient  
	optimizer.update(params, grads) 
     
# Set the area 
    x = np.arange(-10, 10, 0.01) 
    y = np.arange(-5, 5, 0.01) 
     
    X, Y = np.meshgrid(x, y)  
    Z = f(X, Y) 
     
    mask = Z > 7 
    Z[mask] = 0 
     
    # plot  
    plt.subplot(1, 4, idx) 
    idx += 1 
    plt.plot(x_history, y_history, 'o-', color="orange") 
    plt.contour(X, Y, Z)     
plt.show()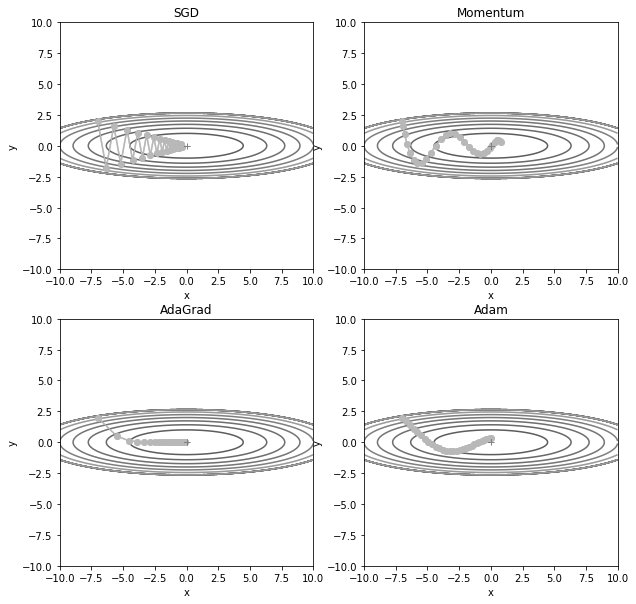

This is the output of code above. You can check how the optimizers go to the global minimum.