Convolution Layer with Numpy

Basic Forward and Backward Propagation of Convolution Layer in Python

Convolution layer

In the field of image processing, the Convolution layer is the core building block of a Convolutional Neural Network. The primary purpose of Convolution layer is to extract features from the input image. The Convolution layer parameters consist of a set of learnable filters (kernels or feature detectors).

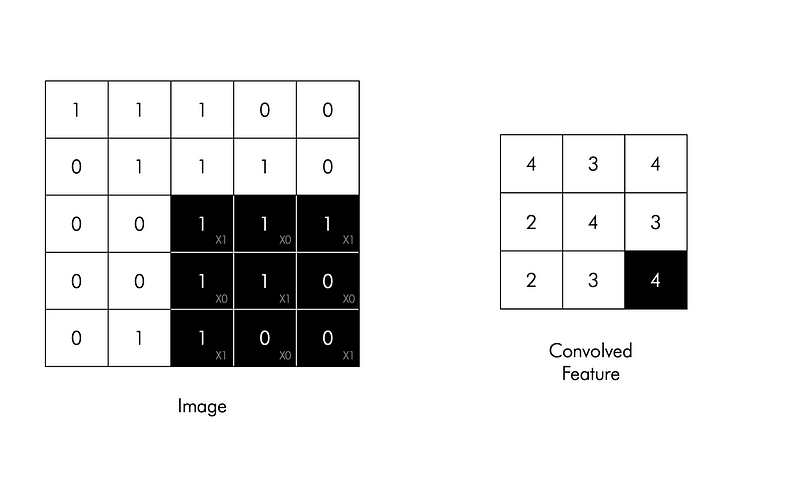
Filters are used for recognizing patterns throughout the entire input image. Convolution works by sliding the filter over the input image and along the way we take the dot product between the filter and chunks of the input image.

Matrix and Tensor

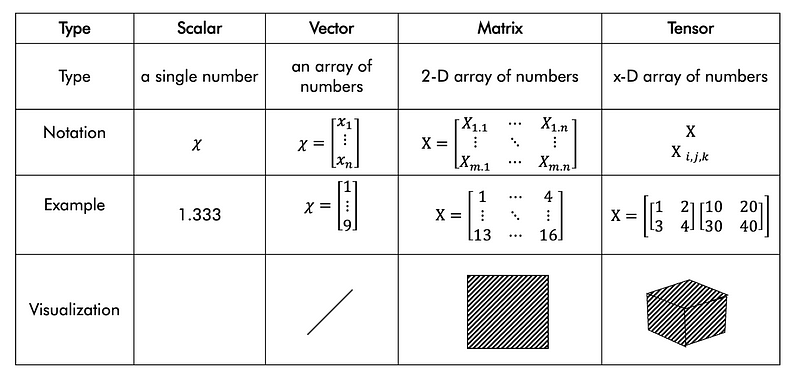
Matrix is a tabular format in which numbers can be represented.

Tensor is like a function, i.e. is linear in nature. It describes an object that is in space. Tensors are of different types. 0 Rank tensors is scalars. 2nd Rank tensors is 2-D arrays which is a matrix.

im2col and col2im

im2col

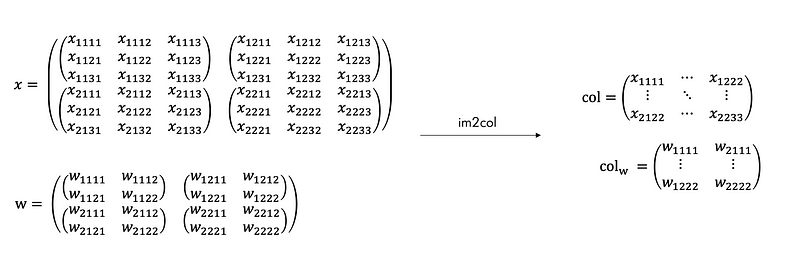
im2col is a technique where we take each window, flatten it out and stack them as columns in a matrix. The current general convolutional layer acceleration method is to use the image to column (im2col) algorithm to split the input image into a column matrix, then use the general matrix multiplication (GEMM) to perform matrix multiplication on the column vector and the convolution kernel.

def im2col(input_data, filter_h, filter_w, stride=1, pad=0): 
    """

Parameters 
    ---------- 
    input_ Data: input data composed of 4-dimensional arrays (data volume, channel, height and length) 
    filter_ H: filter high 
    filter_ W: length of filter 
    Stripe: stride 
    Pad: fill

Returns 
    ------- 
    Col: 2-dimensional array 
    """ 
    N, C, H, W = input_data.shape 
    out_h = (H + 2*pad - filter_h)//stride + 1 
    out_w = (W + 2*pad - filter_w)//stride + 1

img = np.pad(input_data, [(0,0), (0,0), (pad, pad), (pad, pad)], 'constant') 
    col = np.zeros((N, C, filter_h, filter_w, out_h, out_w))

for y in range(filter_h): 
        y_max = y + stride*out_h 
        for x in range(filter_w): 
            x_max = x + stride*out_w 
            col[:, :, y, x, :, :] = img[:, :, y:y_max:stride, x:x_max:stride]

col = col.transpose(0, 4, 5, 1, 2, 3).reshape(N*out_h*out_w, -1) 
    return col

After expanding the input data with im2col, you only need to expand the filter (weight) of the convolution layer vertically into one column and calculate the product of the two matrices.

The weights of the convolution layer are similarly stretched out into rows. After the image and the kernel are converted, the convolution can be implemented as a simple matrix multiplication.

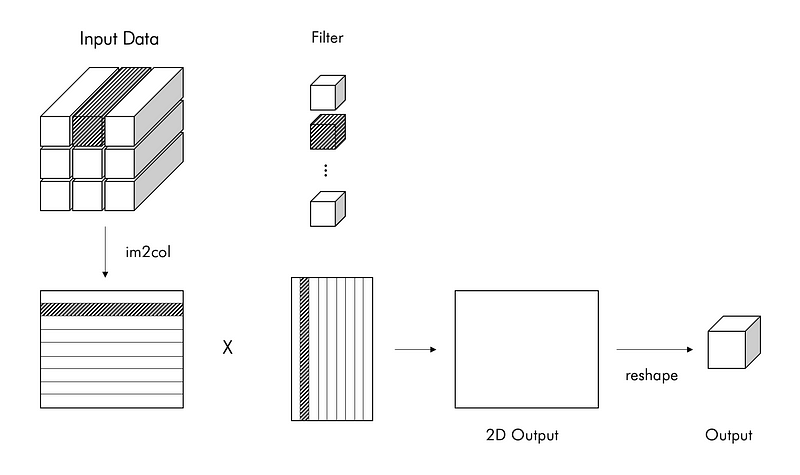
col2im

col2im operation is needed during back propagation. This is for reshaping this multiplied matrix back to an image at the end.

def col2im(col, input_shape, filter_h, filter_w, stride=1, pad=0): 
    """

Parameters 
    ---------- 
    col : 
    input_ Shape: the shape of the input data (for example: (10, 1, 28, 28)) 
    filter_h : 
    filter_w 
    stride 
    pad

Returns 
    -------

""" 
    N, C, H, W = input_shape 
    out_h = (H + 2*pad - filter_h)//stride + 1 
    out_w = (W + 2*pad - filter_w)//stride + 1 
    col = col.reshape(N, out_h, out_w, C, filter_h, filter_w).transpose(0, 3, 4, 5, 1, 2)

img = np.zeros((N, C, H + 2*pad + stride - 1, W + 2*pad + stride - 1)) 
    for y in range(filter_h): 
        y_max = y + stride*out_h 
        for x in range(filter_w): 
            x_max = x + stride*out_w 
            img[:, :, y:y_max:stride, x:x_max:stride] += col[:, :, y, x, :, :]

return img[:, :, pad:H + pad, pad:W + pad]

Convolution Layer

Convolution Layer is consist of forward and backward propagation.

def __init__(self, W, b, stride=1, pad=0): 
		""" 
    Parameters 
    ---------- 
    w : filter 
    b : bias (vector)

"""		 
        self.W = W 
        self.b = b 
        self.stride = stride 
        self.pad = pad 
         
        # temporary variables in backward() 
        self.x = None    
        self.col = None 
        self.col_W = None 
         
        # gradient of weight and bias  
        self.dW = None 
        self.db = None

Forward propagation

After expanding the input data with im2col, you need to expand the filter (weight) of the convolution layer vertically into one column and calculate the product of the two matrices.

def forward(self, x): 
        """ 
        Parameters 
        ---------- 
        x : input data (4D tensor) 
        FN : filter no. 
        C : channel 
        FH : filter height 
        FW : filter width 
        self.W : filter (4D tensor) 
        N : the number of input data in a batch (Batch size) 
        H, W : height and width of input data  
        out_h, out_w : height and width of ouput data (after convolution) 
        ------- 
        out : output images 
        """	 
        FN, C, FH, FW = self.W.shape 
        N, C, H, W = x.shape 
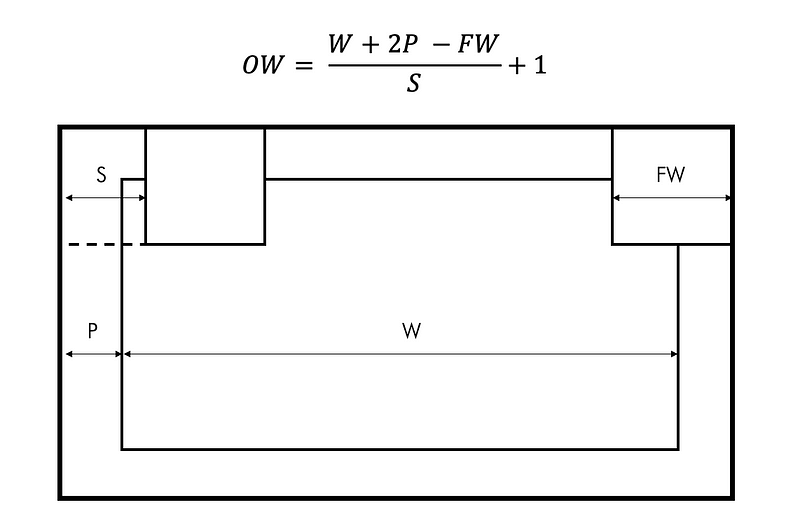
        out_h = 1 + int((H + 2*self.pad - FH) / self.stride) 
        out_w = 1 + int((W + 2*self.pad - FW) / self.stride)

col = im2col(x, FH, FW, self.stride, self.pad) 
        col_W = self.W.reshape(FN, -1).T

out = np.dot(col, col_W) + self.b 
        out = out.reshape(N, out_h, out_w, -1).transpose(0, 3, 1, 2)

self.x = x 
        self.col = col 
        self.col_W = col_W

return out

Backward propagation

As for the code of back propagation of convolution layer, col2im is used, which is the inverse process of im2col.

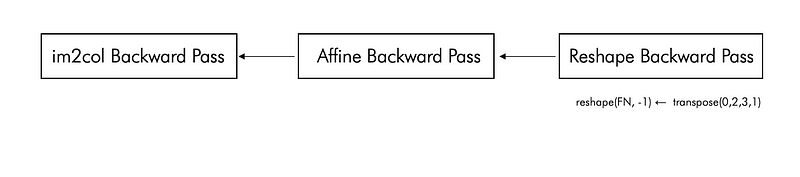
The transpose operation will change the order of the axes of the multidimensional array. For example, transpose (0, 3, 1, 2) is to change the axes of the original 0, 1, 2, 3 positions to the positions of the input parameters.

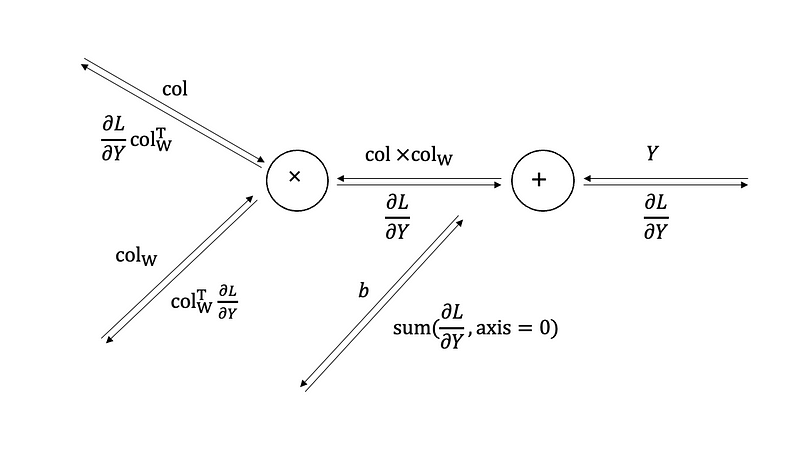
def backward(self, dout):

FN, C, FH, FW = self.W.shape 
        dout = dout.transpose(0,2,3,1).reshape(-1, FN)

self.db = np.sum(dout, axis=0) 
        self.dW = np.dot(self.col.T, dout) 
        self.dW = self.dW.transpose(1, 0).reshape(FN, C, FH, FW)

dcol = np.dot(dout, self.col_W.T) 
        dx = col2im(dcol, self.x.shape, FH, FW, self.stride, self.pad)

return dx

Convolution is a simple mathematical operation that is fundamental to many common image processing operators. I hope this post help you do a great exercise using the convolution layer from scratch.