Batch Normalization

Understanding Batch Normalization with Codes Explained

What is Batch Normalization?

Normalization means normalizing the data dimensions so that they are of approximately the same scale. Batch normalization is a technique for training very deep neural networks that normalizes the contributions to a layer for every mini-batch. Batch Norm is an essential part of the most of deep learning implementation.

Batch Normalization is normalizing the hidden units activation values so that the distribution of these activations remains same during training. Batch Normalization has the impact of settling the learning process and drastically decreasing the number of training epochs required to train deep neural networks.

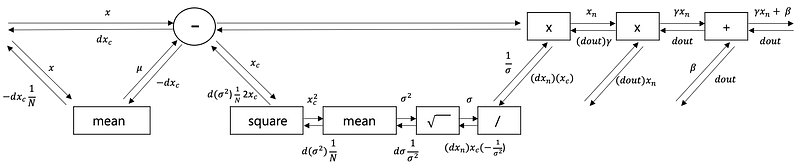
We will assume that X is of size [N x D]. N is the number of data and D is their dimensionality. To get variance, we need to subtract the mean across every individual feature in the data.

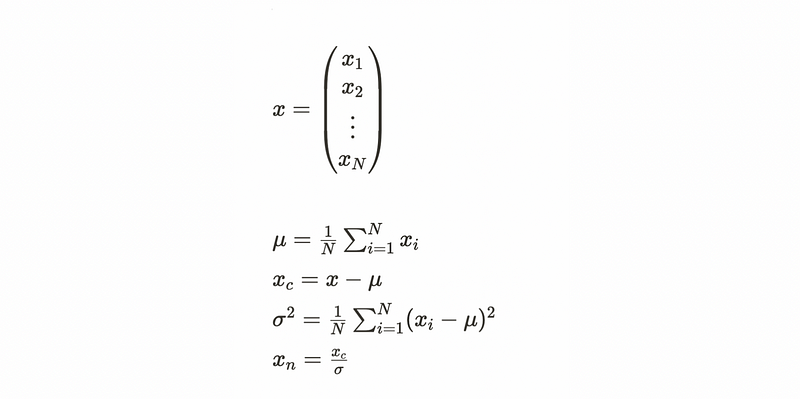
Gamma and Beta are learned along with the other parameters of the network. There would be update rule for gamma and beta and this update rule would depend upon the derivative of the loss function with respect to gamma and beta.

Advantages of Batch Normalization

Here are some benefits of Batch Normalization:

• The model is less delicate to hyperparameter tuning. That is, though bigger learning rates prompted non-valuable models already, bigger LRs are satisfactory at this point.
• Shrinks internal covariant shift.
• Diminishes the reliance of gradients on the scale of the parameters or their underlying values.
• Weight initialization is a smidgen less significant at this point.
• Dropout can be evacuated for regularization.

Batch Normalization Layer

Batch Normalization normalizes batch data (output of Affine or Conv) before activation. Batch Normalization Layer is consist of forward pass and backward pass. The codes are from the book ‘Deep Learning From Scratch’, published in September 2019.

Initialization of Batch Normalization Layer

Temporary variables in forward() and backward() defined in the initialization part.

class BatchNormalization:

def __init__(self, gamma, beta, momentum=0.9, running_mean=None, running_var=None): 
        self.gamma = gamma # scale after normalization 
        self.beta = beta # shift after normalization 
        self.momentum = momentum # smoothing factor of EMA, momentum * newest value 
         
				# temporary variables in forward() 
				self.input_shape = None # Conv:4dim, Affine:2dim

# mean and variance for test session  
        self.running_mean = running_mean  
        self.running_var = running_var   
         
        # temporary variables in backward() 
        self.batch_size = None 
        self.xc = None # centered batch data 
        self.std = None 
        self.dgamma = None 
        self.dbeta = None

Forward Pass of Batch Normalization Layer

Forward Pass has two parts. The second one(__forward) is the actual forward process of batch normalization.

def forward(self, x, train_flg=True): #train_flg=False when testing  
        self.input_shape = x.shape # hold original shape here 
        if x.ndim != 2: # If the previous layer is not Affine(ndim=2) 
            N, C, H, W = x.shape 
            x = x.reshape(N, -1)  
        out = self.__forward(x, train_flg) 
        return out.reshape(*self.input_shape) # recover the shape of x after normalization

def __forward(self, x, train_flg): 
        if self.running_mean is None: 
            N, D = x.shape 
						# In the first iteration,setting moving average and var as 0. 
            self.running_mean = np.zeros(D) 
            self.running_var = np.zeros(D) 
                         
        if train_flg: # When training 
            mu = x.mean(axis=0) # find mean for each column 
            xc = x - mu # mean subtraction  
            var = np.mean(xc**2, axis=0) 
            std = np.sqrt(var + 10e-7) # + 10e-7 protects the vale from 0 
            xn = xc / std #normalize 
             
            self.batch_size = x.shape[0] 
            self.xc = xc 
            self.xn = xn 
            self.std = std 
            self.running_mean = self.momentum * self.running_mean + (1-self.momentum) * mu 
            self.running_var = self.momentum * self.running_var + (1-self.momentum) * var             
        else: # When testing 
            xc = x - self.running_mean 
            xn = xc / ((np.sqrt(self.running_var + 10e-7))) 
             
        out = self.gamma * xn + self.beta # gamma and beta are defined after training 
        return out

Backward Pass of Batch Normalization Layer

This process is to find dgamma and dbeta, which is used to update beta and gamma.

def backward(self, dout): 
        if dout.ndim != 2: 
            N, C, H, W = dout.shape 
            dout = dout.reshape(N, -1)

dx = self.__backward(dout)

dx = dx.reshape(*self.input_shape) 
        return dx

def __backward(self, dout): 
        dbeta = dout.sum(axis=0) 
        dgamma = np.sum(self.xn * dout, axis=0) # Hadamard product 
        dxn = self.gamma * dout 
        dxc = dxn / self.std  
        dstd = -np.sum((dxn * self.xc) / (self.std * self.std), axis=0) 
        dvar = 0.5 * dstd / self.std 
        dxc += (2.0 / self.batch_size) * self.xc * dvar 
        dmu = np.sum(dxc, axis=0) 
        dx = dxc - dmu / self.batch_size 
         
        self.dgamma = dgamma 
        self.dbeta = dbeta 
         
        return dx

Batch Norm is a very useful layer. If you are interested in Deep Learning, you will for sure have to get familiar with this method. I hope this post gives you a good understanding of how Batch Norm works.